ديسيبل تعليمي: ديسيبل و ديسيبل مقابل كسب وميلي واط

مفهوم الديسيبل (ديسيبل) هو مفهوم صعب ومربك لشخص ما يجري عرضه عليه. إن الجمع بين مواصفات الكسب ، والطاقة ، والجهد (والتيار ، ولكن ليس في كثير من الأحيان) التي تمزج بين ديسيبل ، ديسيبل ، ديسيبل ، واتس ، ميلي واط ، فولط ، ميليتولتس ، إلخ ، غالبًا ما تتطلب التحويل ذهابًا وإيابًا بين القيم الخطية وقيم ديسيبل. سيساعد هذا البرنامج التعليمي الموجز في توضيح الفرق بين العمل بالديسيبل والعمل باستخدام القيم الخطية.

تم وضع اللوغاريتمات (logs) لأول مرة في أوائل 1600s من قبل عالم الرياضيات الاسكتلندي John Napier ، كأداة لتبسيط عمليات الضرب والقسمة من خلال تحويلها إلى عمليات الجمع والطرح بشكل أسرع وأقل عرضة للخطأ ، على التوالي. أصبح هذا ممكنًا نظرًا للطريقة التي يمكن بها مضاعفة رقمين معبراً عنها كأرقام أساسية مماثلة مع الأس ، وذلك بمجرد إضافة الأسات معًا. يتم إنجاز تقسيم هذه الأرقام نفسها بطرح الأسس. إنه أحد قوانين الأسس ، ويبدو كالتالي:

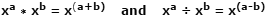
باستخدام الأرقام الفعلية كمثال ، حيث x = 10 ، a = 4 ، b = 1:

قانون الأسس يعمل مع أي رقم أساسي ، وليس فقط 10. لخفة الظل:

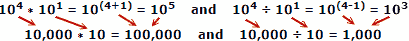
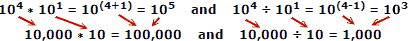
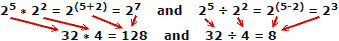
يميل الأشخاص إلى ارتكاب أخطاء أقل عند إضافة وطرح الأرقام ، لذلك فإن ميزة اللوغاريتمات واضحة. تذكر أنه تم تطوير اللوغاريتمات قبل توفر أجهزة الكمبيوتر الميكانيكية أو الإلكترونية. تستغل قاعدة الشرائح خصائص اللوغاريتمات لحسابها ، لكن هذا موضوع رئيسي منفصل.

هذه أمثلة بسيطة ، ولكن تمسك بأي قاعدة أو أسي. في غياب الآلة الحاسبة ، لكي تكون مفيدًا للتطبيق العام ، تحتاج إلى جدول أرقام ولوغاريتمات معادلة لها. تملأ جداول السجل المبكرة وحدات التخزين ، اعتمادًا على التباعد بين الأرقام (1.000 ، 1.001 ، 1.002 ، 1.003 ، مقابل 1.0 ، 1.1 ، 1.2 ، 1.3 ، وما إلى ذلك). الخبر السار لمنشئي جداول اللوغاريتم هو أن "العقد" واحد فقط من الأرقام (على سبيل المثال ، 1 من خلال 10) مطلوب لأن كل عقد سابق أو ثانوي هو مضاعف بسيط لقوة 10.

ملاحظة: أستخدم قاعدة 10 في هذه المناقشة لأن هذا هو أساس نظام الأرقام المشترك الخاص بنا - ومن هنا يأتي مصطلح "لوغاريتم مشترك" لسجلات 10 الأساسية. ربما تكون قد سمعت عن اللوغاريتمات الطبيعية ، التي تستخدم قاعدة e ، لكن e لا يتم استخدامه كثيرًا عند حساب الطاقة الكهربائية والجهد والكميات الحالية (على الرغم من استخدامه عند تضمين زوايا الطور ، أي هوية Euler). تتم كتابة اللوغاريتمات الطبيعية بالرمز ln (x) دون الحرف 'e' ، بينما عادةً ما يتم كتابة اللوغاريتمات 10 الأساسية ببساطة كـ log (x) بدون منخفض 10 ؛ أي ليس loge (x) أو log10 (x) ، على التوالي.

لكل قاعدة = جدول سجل 10:

شبه رسم لوغاريتمي 5 Cycles Engineering Graph Paper - RF Cafe الاستثناء والحالة الخاصة logx (0) = غير محدد. هذا لأنه لا توجد سلطة يمكنك من خلالها رفع أي رقم والحصول على 0 (صفر). يمكنك الاقتراب من الصفر ، ولكن لا يمكنك الوصول إلى الصفر. لن يكون هناك أبدًا الرقم صفر المعروض على مقياس السجل ؛ عادة ما يتم تشغيلها من قوة 10 إلى قوة أخرى من عشرة. يظهر مثال على ورقة الرسم البياني سجل على اليمين. لديها 5 "دورات" أو "عقود" من النطاق. لاحظ أنه لا يوجد صفر على المحور ص.

لوغاريتم الأساس 10 (الشائع) للرقم ، إذن ، هو الأس الذي يجب رفع 10 إليه للحصول على هذا الرقم. بمعنى آخر ، بما أن 10 مرفوعة إلى قوة 2 تساوي 100 (102 = 100) ، فإن سجل 10 الأساسي لـ 100 هو 2 (log10 100 = 2).

هذا هو القانون الأساسي لوغاريتمات:


تنفيذ نفس الضرب والأقسام كما فعلت في أعلى الصفحة باستخدام اللوغاريتمات الفعلية:



هذا جيد ، لكن ما انتهى إليه الأمر هو لوغاريتم الرقم الذي تبحث عنه. سؤال: باستثناء مثال بسيط مثل هذا ، كيف تحصل على الإجابة التي تحتاجها؟ الإجابة: ابحث عن antilogarithm (antilog) للنتيجة. في هذه الحالة:

قد يبدو الشكل الأكثر صرامة والأرجح مع الأرقام التي لا تمثل عددًا صحيحًا من القوى في 10 ، كما يلي:




 آلة حاسبة HP-35 (ويكيبيديا) - RF CafeSince لوغاريتم 'x' يساوي 1.8444 ، antilog يساوي 'x' ، وهو 69.9



لقد استخدمت الآلة الحاسبة الخاصة بي للبحث عن السجلات و antilogs لتلك الأرقام ، ولكن قبل 1972 عندما قدمت Hewlett Packard (HP) حاسوبها العلمي HP-35 ، الشخص العادي دون الوصول إلى كمبيوتر حاسب رئيسي للشركة أو الجامعة يحتاج إلى استخدام سجل الجدول لأداء مثل هذه الحسابات.

من يزعج استخدام اللوغاريتمات اليوم ، قد تسأل؟ الكثير من الأشخاص ، بمن فيهم أنا ، غالبًا عند حساب معلمات النظام المتتالية مثل رقم الضوضاء (NF) ونقاط الاعتراض (IP). إضافة وطرح بسيط للكسب dB وقيم dBm للقدرة لا تعمل مع NF و IP. تستخدم الصيغ الحاكمة الضرب وتقسيم الكسب الخطي وقيم القدرة ، الأمر الذي يتطلب أولاً تحويل dB و / أو dBm إلى أرقام خطية (نسبة الكسب و mW) باستخدام antilogs ، وإجراء العمليات الحسابية المتتالية ، ثم تحويل النتيجة مرة أخرى إلى dB و / أو ديسيبل باستخدام سجلات.

ليست كل عمليات تتالي النظام تتطلب تحويل جيئة وذهابا. على سبيل المثال ، إذا كانت هناك حاجة فقط لكسب النظام الكلي و / أو مستوى قدرة الخرج ، فيمكن إجراء العمليات الحسابية إما باستخدام وحدات خطية (mW ومضاعفات) أو وحدات لوغاريتمية (dBm و dB ، على التوالي).

تعريف "ديسيبل" و "ديسيبل"

يتم تعريف ديسيبل (ديسيبل) في الهندسة الكهربائية بأنها 10 أضعاف لوغاريتم 10 الأساسي لنسبة بين مستويين للطاقة ؛ على سبيل المثال ، Pout / Pin (ربح ، بمعنى آخر). لخفة الظل:

لذلك يتم التعبير عن جميع المكاسب التي تزيد عن 1 بالديسيبل الموجب (> 0) ، ويتم التعبير عن المكاسب التي تقل عن 1 بالديسيبل السالب (<0). لاحظ أنه بالنسبة للحالات التي يواجهها معظمنا ، يجب أن تكون النسبة الخطية لـ P1 / P2 عددًا موجبًا (> 0) نظرًا لأن لوغاريتم 0 غير محدد ولوغاريتم الأرقام السلبية معقدة (تحتوي على جزء حقيقي وجزء وهمي ). ومع ذلك ، يمكن لقيمة dB نظريًا أن تأخذ أي قيمة بين و + ، بما في ذلك 0 ، وهو كسب قدره 1 [10 * log (1) = 0 dB].

'dBm' هي وحدة طاقة تستند إلى ديسيبل تتم الإشارة إليها على 1 mW. نظرًا لأن 0 dB من الكسب تساوي كسب 1 ، فإن 1 mW من الطاقة تزيد 0 dB عن 1 mW أو 0 dBm. وبالمثل ، فإن وحدة القدرة dBW هي ديسيبل بالنسبة إلى 1 W للطاقة.


وفقًا لذلك ، تكون جميع قيم dBm أكبر من 0 أكبر من 1 mW ، وجميع قيم dBm أقل من 0 أصغر من 1 mW (انظر الشكل 1). على سبيل المثال ، + 3.01 dBm أكبر من 3.01 dB 1 ؛ أي ، أو 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm أقل من 3.01 dB من 1 mW ؛ أي ، أو 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

يقدم الجدول التالي بعض الأمثلة العددية حتى تتمكن من رؤية العلاقة بين mW و dBm. نفس مجموعة القيم المرسومة على مقياس لوغاريتمي ستنتج خطًا مستقيمًا. بسبب العلاقة اللوغاريتمية ، يقوم الرسم البياني بتجميع القيم الأصغر مقابل المحور العمودي الأيسر. نسخة مكبرة من منطقة 0 إلى 1 mW غير مدمجة للوضوح.

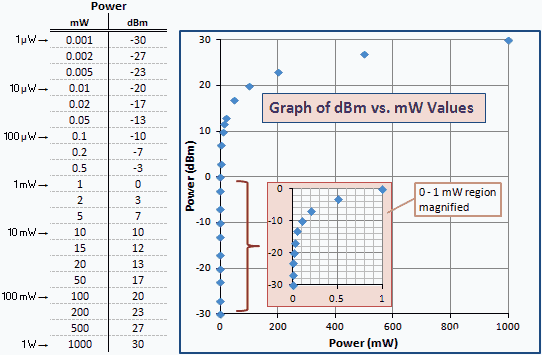
الشكل 1 - رسم بياني للقدرة بوحدات dBm مقابل mW

الشكل 2 هو جدول ورسم بياني لنسب الكسب dB مقابل الكسب الخطي مماثل للقيمة dBm مقابل mW في الشكل 1. لاحظ أن الأرقام والمنحنيات متطابقة تمامًا ؛ يتم تغيير تسميات المحور فقط. ذلك لأن dBm هي وحدة قدرة معبرا عنها بوحدة dB بالنسبة إلى 1 mW (0 dBm).

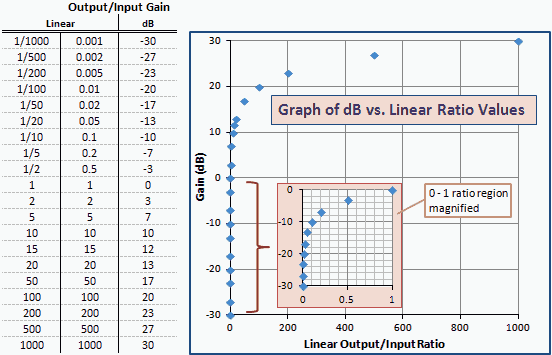
الشكل 2 - الرسم البياني للربح بوحدات dBm مقابل النسبة الخطية

في الأساس ، الكسب هو عامل الضرب (أو القسمة). على سبيل المثال ، قد يكون للمكبر مكسب يزيد الإشارة بعامل 4 (أي 4x) من الإدخال إلى الخرج (انظر الشكل 3). إذا تم إدخال إشارة 1 mW (0 dBm) في مكبر الصوت ، فسيخرج 1 mW * 4 = 4 mW. فيما يتعلق بالديسيبل ، فإن عامل 4 يعادل 10 * log (4) = 6.02 dB ، لذلك 0 dBm بالإضافة إلى 6.02 dB من عوائد الكسب + 6.02 dBm في الخرج.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

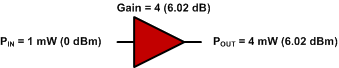
الشكل. 3 - كسب مكبر للصوت مفرد.

الجمع بين المكاسب (الخطية والديسيبل) ث / القيمة الإيجابية

إذا كان مضخم صوت ذو كسب 4 متسلسلًا مع مضخم صوت ثاني مع كسب 6 ، فإن إجمالي الكسب هو 4 * 6 = 24. فيما يتعلق بالديسيبل ، فإن عامل 6 مكافئ لـ 10 * log (6) = 7.78 dB ، وعامل 24 مكافئ لـ 10 * log (24) = 13.8 dB.

تمامًا مثل 4 x 6 = 24 (الكسب الخطي) ، 6.02 dB + 7.78 dB = 13.8 dB (كسب الديسيبل).

إذا تم إدخال إشارة 1 mW (0 dBm) في مكبر الصوت ، فسيخرج 4 mW من مكبر الصوت الأول ، ويخرج 24 mW من مكبر الصوت الثاني. انظر الشكل. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

الشكل 4 - كسب مكبر الصوت المزدوج المتتالي.

الجمع بين الربح والخسارة (الخطي والديسيبل)
يوضح هذا المثال التالي ما يحدث عند مواجهة ربح <1 (خسارة) ، حيث يتم وضع المخفف مع ربح 1/6 بعد مكبر الصوت الأول بدلاً من وجود مضخم ثانٍ. انظر الشكل 5.
4 * 1 / 6 = 2 / 3 (كسب خطي). بالمثل 6.02 dB - 7.78 dB = −1.76 dB (كسب الديسيبل).
كما في المثال السابق ، إذا تم تغذية إشارة 1 mW (0 dBm) في مكبر الصوت مع كسب 4 ، عندئذٍ تخرج 4 mW. ينتقل ذلك 4 mW بعد ذلك إلى المخفف مع كسب خطي من 1 / 6 ويخرج عند مستوى طاقة 4 / 6 mW (2 / 3 mW).
الكسب الإجمالي في هذه الحالة هو 4 / 6 = 2 / 3 ، وبالتالي فإن طاقة الخرج ستكون في الواقع أقل من طاقة الإدخال.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 ديسيبل

الشكل 5 - كسب مكبر الصوت المتتالي والمخفف.

12 mW + 34 mW + 8 mW + 20 dB

معلومات تكميلية عن اللوغاريتمات
لوغاريتمات المنتجات
تنص خاصية اللوغاريتمات المستخدمة أعلاه ضمنيًا على ما يلي ، وهي أساس القدرة على إضافة وطرح قيم اللوغاريتم بدلاً من ضرب معادلاتها الخطية.

قد يمثل 'h * j / k * m / n' سلسلة من المكونات التي تحتوي على ثلاثة أجهزة (h و j و m) لكل منها ربح> 1 وجهازان (k و n) لكل منهما ربح <1 (انظر الشكل 6). يمكن حساب إجمالي كسب النظام إما بضرب جميع قيم الكسب الخطي معًا أو إضافة جميع قيم كسب الديسيبل معًا.

الشكل. 6 - المكونات المتتالية

لوغاريتمات الأس
التالي مهم لفهم سبب كسب الطاقة من حيث الطاقة 10 * log (Pout / Pin) dB ، بينما كسب الطاقة من حيث الجهد هو 20 * log (Vout / Vin) dB.


وهذا هو السبب في أن cf تساوي c مضروبة بحد ذاتها "f" مرات. على سبيل المثال ، إذا كانت f = 4:


كسب القوة على أساس القوة مقابل كسب السلطة على أساس الجهد
كسب الطاقة هو Pout / Pin ، وزيادة الجهد هو Vout / Vin. يتم تعريف كسب الطاقة على أساس نسبة الطاقة بالديسيبل بأنه سجل 10 * (Pout / Pin). كسب الطاقة من حيث الجهد ، هو [(Vout2 / R) / (Vin2 / R)] ، بما أنه وفقًا لقانون أوم P = V2 / R. تقوم 'R' في القواطع بإلغاء ترك Vout2 / Vin2 ، والذي يساوي (Vout / Vin) 2 ، كما هو محدد بواسطة قاعدة الأسس التي تقول ac / bc = (a / b) c. بالتالي:

ملاحظة هامة: كسب الجهد من حيث الجهد هو 10 * log (Vout / Vin) dB ، كما هو الحال مع زيادة الطاقة من حيث الطاقة. يتم تطبيق معادلة 20 * log (Vout / Vin) dB فقط عند التعبير عن زيادة الطاقة من حيث الجهد. هذه هي نقطة مشتركة من الارتباك.


لا توجد عملية تعسفية في الرياضيات ، وهذا ينطبق على سبب تصوير فقدان طاقة الإشارة (الكسب <1) على أنه قيمة سالبة ، وبالتالي يتم طرحه أثناء الحساب المتتالي. إنه عرض بسيط ، لكن جدير بالذكر.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

إذا كنت ترغب في بناء محطة راديو ، فقم بتعزيز جهاز إرسال راديو FM أو تحتاج إلى أي محطة أخرى معدات FM ، لا تتردد في الاتصال بنا: [البريد الإلكتروني محمي].

اترك رسالة 

قائمة الرسالة